Feedback Controllers

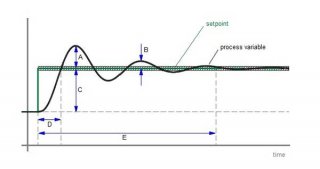A feedback controller measures the output of a process and then manipulates the input as needed to drive the process variable toward the desired setpoint. A controller reacts to setpoint changes initiated by the operators as well as random disturbances to the process variable caused by external forces. It repeats this measure-decide-actuate sequence over and over until the process variable matches the setpoint.

Unfortunately, that’s easier said than done. The inertia of the process prevents the controller from altering the process variable instantaneously, so the controller has to settle for “close enough, ” at least in the near term. Exactly how close depends on how the controller is designed, and the design is typically based on how much slack between the process variable and the setpoint is acceptable for a particular application.

Case in point

Consider, for example, a baking process where the dough in the oven must be heated without scorching. When an operator bumps up the oven temperature at the beginning of a batch, the controller must turn up the heat enough to reach the required baking temperature but without overdoing it. In this application, close equates to limited overshoot or, “as near as possible to the setpoint without exceeding it too much.”

In contrast, the process of warming up the interior of a luxury car on a cold day requires more speed than accuracy. The driver of the car typically wants the interior temperature to reach a comfortable range as soon as possible, even if that means the car’s temperature controller has to raise the temperature so quickly that it overshoots the setpoint. Here, close equates to minimum rise time or, “as near as possible to the setpoint as soon as possible.”

Closeness can be quantified in terms of an objective function or a performance measure that shows with a single statistic how well the process variable has matched the setpoint. There is a variety of performance measures to choose from, depending on which definition of “close” is most appropriate for a particular application. The “Basic performance measures” graphic shows four of the more straightforward performance measures often used in applications where the setpoint changes frequently.

Controller design

Conversely, the chosen performance measure dictates how the controller should be designed in order to achieve the desired closed-loop results. The minimal overshoot necessary for the baking application would require that the controller be tuned to be especially conservative about how it manipulates the process. For the car temperature application, the controller would have to be tuned to be more aggressive in order to achieve the fastest possible rise time.

This is a fairly straightforward calculation when the chosen performance measure comes with a set of formulae that translate observable characteristics of the process directly into controller settings. For example, the classic Ziegler-Nichols tuning rules use the ultimate gain and ultimate period of the process to generate PID parameters that will endow the controller with the ability to produce a ¼ decay ratio in response to a setpoint change.

Unfortunately, it’s not usually that easy. Most performance measures require more extensive calculations to determine the tuning parameters that will provide optimal results. The integrated performance measures shown in the second graphic are prime examples.

Trial and error

Designing a controller to optimize any of these performance measures typically involves a mathematical model of the process, an off-line simulation program, and an iterative trial-and-error test. The designer first guesses at a set of tuning parameters that could conceivably yield optimal results and then configures a simulation of a controller thus tuned operating on a model of the process.