Mechanical control Systems Examples

There are various types of physical systems namely we have

1. Mechanical system.
2. Electrical system.
3. Electronic system.
4. Thermal system.
5. Hydraulic system.
6. Chemical system etc.

Before I describe these systems in detail let us know, what is the meaning of modeling of the system? is the process of drawing the block diagram for these types of systems in order to determine the performance and the transfer functions.

Now let us describe mechanical and electrical type of systems in detail. We will derive analogies between mechanical and electrical system only which are most important in understanding the theory of control system.

Mathematical Modelling of Mechanical Systems

We have two types of mechanical systems. Mechanical system may be a linear mechanical system or it may be a rotational mechanical type of system. In linear mechanical type of systems we have three variables -

1. Force which is represented by ‘F’.
2. Velocity which is represented by ‘V’.
3. Linear displacement represented by ‘X’

And also we have three parameters-

1. Mass which is represented by ‘M’.
2. Coefficient of viscous friction which is represented by ‘B’.
3. Spring constant which is represented by ‘K’.

In rotational mechanical type of systems we have three variables-

1. Torque which is represented by ‘T’.
2. Angular velocity which is represented by ‘ω’
3. Angular displacement represented by ‘θ’

And also we have two parameters -

1. Moment of inertia which is represented by ‘J’.

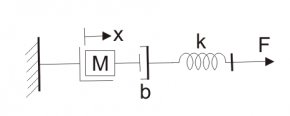
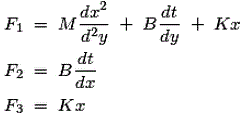Now let us consider the linear displacement mechanical system which is shown below- We have already marked various variables in the diagram itself. We have x is the displacement as shown in the diagram. From the Newton’s second law of motion, we can write force as- From the diagram we can see that the, On substituting the values of F1, F2 and F3 in the above equation and taking the Laplace transform we have the transfer function as, This equation is mathematical modelling of mechanical control system.

Mathematical Modelling of Electrical System

In electrical type of systems we have three variables -

1. Voltage which is represented by ‘V’.
2. Current which is represented by ‘I’.
3. Charge which is represented by ‘Q’.

And also we have three parameters which are active and passive elements -

1. Capacitance which is represented by ‘C’.
2. Inductance which is represented by ‘L’.

Now we are in condition to derive analogy between electrical and mechanical types of systems. There are two types of analogies and they are written below:

Force Voltage Analogy : In order to understand this type of analogy, let us consider a circuit which consists of series combination of resistor, inductor and capacitor. A voltage V is connected in series with these elements as shown in the circuit diagram. Now from the circuit diagram and with the help of KVL equation we write the expression for voltage in terms of charge, resistance, capacitor and inductor as, Now comparing the above with that we have derived for the mechanical system we find that-

1. Force is analogous to voltage V.
2. Displacement (x) is analogous to charge (Q).
3. Coefficient of friction (B) is analogous to resistance R and
4. Spring constant is analogous to inverse of the capacitor (C).

A voltage E is connected in parallel with these elements as shown in the circuit diagram. Now from the circuit diagram and with the help of KCL equation we write the expression for current in terms of flux, resistance, capacitor and inductor as, Now comparing the above with that we have derived for the mechanical system we find that,

1. Mass (M) is analogous to Capacitor (C).
2. Force is analogous to current I.
3. Displacement (x) is analogous to flux (ψ).
4. Coefficient of friction (B) is analogous to resistance 1/ R and
5. Spring constant K is analogous to inverse of the inductor (L).

This analogy is known as force current analogy.