Control Systems Theory

This simple example, however can be complex to both users and designers of the motor system. It may seem obvious that the motor should start at a higher voltage, so that it accelerates faster. Then we can reduce the supply back down to 10 volts once it reaches ideal speed.

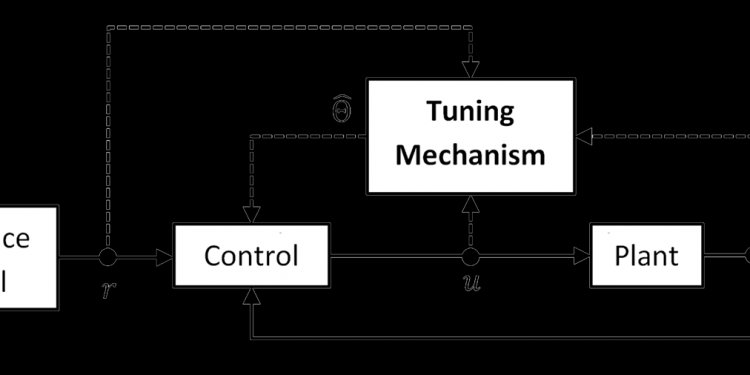
This is clearly a simplistic example, but it illustrates an important point: we can add special "Controller units" to preexisting systems, to improve performance and meet new system specifications.

Here are some formal definitions of terms used throughout this book:

Control System A Control System is a device, or a collection of devices that manage the behavior of other devices. Some devices are not controllable. A control system is an interconnection of components connected or related in such a manner as to command, direct, or regulate itself or another system. Control System is a conceptual framework for designing systems with capabilities of regulation and/or tracking to give a desired performance. For this there must be a set of signals measurable to know the performance, another set of signals measurable to influence the evolution of the system in time and a third set which is not measurable but disturb the evolution. Controller A controller is a control system that manages the behavior of another device or system. Compensator A Compensator is a control system that regulates another system, usually by conditioning the input or the output to that system. Compensators are typically employed to correct a single design flaw, with the intention of affecting other aspects of the design in a minimal manner.

There are essentially two methods to approach the problem of designing a new control system: the Classical Approach, and the Modern Approach.

Classical and Modern[edit]

Classical and Modern control methodologies are named in a misleading way, because the group of techniques called "Classical" were actually developed later than the techniques labeled "Modern". However, in terms of developing control systems, Modern methods have been used to great effect more recently, while the Classical methods have been gradually falling out of favor. Most recently, it has been shown that Classical and Modern methods can be combined to highlight their respective strengths and weaknesses.

Classical Methods, which this book will consider first, are methods involving the Laplace Transform domain. Physical systems are modeled in the so-called "time domain", where the response of a given system is a function of the various inputs, the previous system values, and time. As time progresses, the state of the system and its response change. However, time-domain models for systems are frequently modeled using high-order differential equations which can become impossibly difficult for humans to solve and some of which can even become impossible for modern computer systems to solve efficiently. To counteract this problem, integral transforms, such as the Laplace Transform and the Fourier Transform, can be employed to change an Ordinary Differential Equation (ODE) in the time domain into a regular algebraic polynomial in the transform domain. Once a given system has been converted into the transform domain it can be manipulated with greater ease and analyzed quickly by humans and computers alike.

Modern Control Methods, instead of changing domains to avoid the complexities of time-domain ODE mathematics, converts the differential equations into a system of lower-order time domain equations called State Equations, which can then be manipulated using techniques from linear algebra. This book will consider Modern Methods second.

A third distinction that is frequently made in the realm of control systems is to divide analog methods (classical and modern, described above) from digital methods. Digital Control Methods were designed to try and incorporate the emerging power of computer systems into previous control methodologies. A special transform, known as the Z-Transform, was developed that can adequately describe digital systems, but at the same time can be converted (with some effort) into the Laplace domain. Once in the Laplace domain, the digital system can be manipulated and analyzed in a very similar manner to Classical analog systems. For this reason, this book will not make a hard and fast distinction between Analog and Digital systems, and instead will attempt to study both paradigms in parallel.

Who is This Book For?[edit]

This book is intended to accompany a course of study in under-graduate and graduate engineering. As has been mentioned previously, this book is not focused on any particular discipline within engineering, however any person who wants to make use of this material should have some basic background in the Laplace transform (if not other transforms), calculus, etc. The material in this book may be used to accompany several semesters of study, depending on the program of your particular college or university. The study of control systems is generally a topic that is reserved for students in their 3rd or 4th year of a 4 year undergraduate program, because it requires so much previous information. Some of the more advanced topics may not be covered until later in a graduate program.