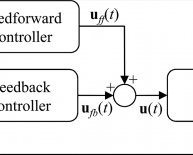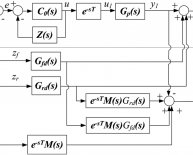
Comparison between feedback and feedforward control system

Figure 1: Example of redundancy, in which different combinations of two effectors achieve the behavioral goal. The observed motor commands (red ellipse) lie close to this solution space or uncontrolled manifold (line) . Feedback mechanisms that only correct task-relevant error (blue errors) can account for this pattern of variability, as variation along the uncontrolled manifold is allowed to accumulate over the movement (minimal intervention principle).

Coordination is tightly related to the concept of redundancy. Redundancy refers to the fact that the motor system usually has more degrees of freedom available than strictly necessary for the achievement of a task. For example, different combinations of elbow and wrist rotation may lead to the same desired position for the endpoint of a hand-held instrument (Vetter et al. 2002). Therefore, multiple combinations of movements from each of a set of effectors will ultimately lead to the same task outcome (Figure ). Coordination is historically viewed as the solution to the “problem of redundancy” (Bernstein 1967), meaning the problem of choosing a movement from the set of redundant possibilities.

A typical characteristic of biological motor control is that movement variability along this task-irrelevant dimension is much higher than along task-relevant dimensions (red ellipse, Figure ). The subspace formed by these task-irrelevant dimensions is therefore often referred to as the uncontrolled manifold (Scholz et al. 1999). Increased variability along the manifold can be explained by feedback mechanisms that follow the minimal intervention principle (Todorov et al. 2002), i.e. that only correct for task-relevant errors and do not reduce variability along the uncontrolled manifold, thereby reducing effort and signal-dependent noise. To achieve this task dependence, the feedback mechanism requires knowledge about the state of both effectors, and about how the movements of each effector influence the outcome variable or goal of the task. In this view, the system actively exploits the redudancy of the system to improve performance (Latash, 2012).

Muscle coordination for index finger movements

Seven muscles, located around its base, pull the index finger in different directions. This muscular system is (at least for low forces) redundant. That is, multiple combinations of muscle activations can produce the same desired force at the tip of the index finger. The variability of activity during force production is not independent across muscles, thereby indicating that these muscles are coordinated. Variability is highest along the uncontrolled manifold, i.e., the subspace of muscle activations that does not change the force at the tip of the index finger. While this structured variability fulfills the criterion of synergy, the results can be explained by coordinative feedback corrections and the minimal intervention principle (Valero-Cuevas et al. 2009).

Temporal coordination of muscle commands

To achieve smooth and coordinated arm movements, the activity of all muscles must be precisely coordinated in time. For single-joint movements, a tri-phasic pattern of muscle activity is observed: After an initial burst of the agonist, the antagonist muscle breaks the movement, followed by an additional burst of the agonist that stabilizes the limb (Hallett et al., 1975). For multi-joint movements in different directions, the onset of shoulder and elbow muscles are finely coordinated in time (Karst and Hasan, 1991). Whether these temporal regularities are an emergent property of a coordination mechanisms, in which the command to each muscle depends on the estimated state of the movement (Diedrichsen et al., 2007), or whether they are caused by an internal timing mechanism, is unclear.

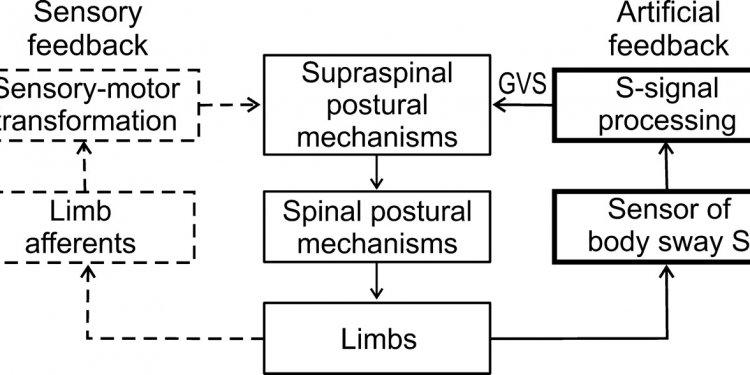
Multi-joint coordination of elbow and shoulder

Figure 2: A positional perturbation to the elbow (black arrow) leads to a local feedback response (elbow torque, red arrow) and a coordinative feedback response in the shoulder joint (shoulder torque, blue arrow). Adapted from (Pruszynski et al. 2011).

The two-joint arm (elbow, shoulder) provides an example, in which coordination is necessary because movement in one effector will result in torques acting on the other. In an elegant experiment, Pruszynski and colleagues (Pruszynski et al. 2011) provide evidence that fast feedback mechanisms actively compensate for this mechanical coupling. In one of their experiments, they delivered a positional perturbation to the elbow joint (Figure, dashed arrow). A local feedback mechanism would react with a torque generated at the elbow joint only (red arrow). However, due to the mechanical coupling in the joint, this would lead to movement of the shoulder. Therefore, to stabilize the shoulder, participants also produce a compensatory shoulder torque (blue arrow) at time latencies as short as 70 ms. Using single-unit recording in primary motor cortex, the authors also found that neurons whose firing rate correlates well with the shoulder torque under static conditions exhibit a response to elbow perturbations at a latency of 50 ms. These motor cortical neurons therefore provide the neuronal manifestation of fast coordinative feedback responses. Thus, the responses of one effector depend on sensory input signaling the perturbation of another effector.

Bimanual coordination

The ability to use both hands simultaneously to manipulate objects is one of the core examples of dexterous motor behaviors in humans. Studies of human bimanual coordination fall broadly into two perspectives. The first one focuses on the phenomenon that movements of the two upper limbs spontaneously synchronize in time and space. The second perspective attempts to illuminate how the two hands achieve coordination to accomplish specific tasks, in which a breaking of symmetry and synchrony is often required.

One of the persistent observations about movements of the two upper limbs is that – unless required by the task – humans tend to initiate movements of the upper limbs in close temporal proximity, often with onset asynchronies of less than 20 ms (Kelso et al. 1979). The tendency to synchronize can also be observed in cyclic movements, such as the repetitive abduction – adduction of the index fingers of the two hands. Under such conditions, the human motor system has a relatively persistent preference for patterns of mirror symmetric movements (Kelso 1984). At higher speeds, the less preferred coordination patterns become unstable and the system spontaneously falls into the mirror-symmetric mode. These phenomena have been successfully explained with a dynamical systems approach to coordination, in which the interaction between the hands is modeled as two coupled oscillators (Haken et al. 1985, Schoener et al. 1986).