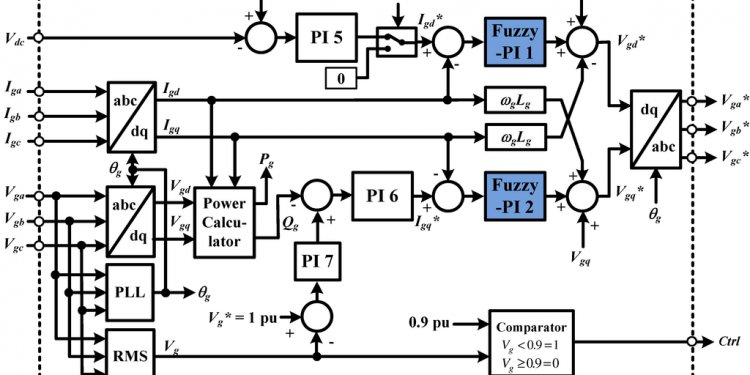
Fuzzy Logic control system

In recent years, the number and variety of applications of fuzzy logic have increased significantly. The applications range from consumer products such as cameras, camcorders, washing machines, and microwave ovens to industrial process control, medical instrumentation, decision-support systems, and portfolio selection.

To understand why use of fuzzy logic has grown, you must first understand what is meant by fuzzy logic.

Fuzzy logic has two different meanings. In a narrow sense, fuzzy logic is a logical system, which is an extension of multivalued logic. However, in a wider sense fuzzy logic (FL) is almost synonymous with the theory of fuzzy sets, a theory which relates to classes of objects with unsharp boundaries in which membership is a matter of degree. In this perspective, fuzzy logic in its narrow sense is a branch of FL. Even in its more narrow definition, fuzzy logic differs both in concept and substance from traditional multivalued logical systems.

In Fuzzy Logic Toolbox™ software, fuzzy logic should be interpreted as FL, that is, fuzzy logic in its wide sense. The basic ideas underlying FL are explained in Foundations of Fuzzy Logic. What might be added is that the basic concept underlying FL is that of a linguistic variable, that is, a variable whose values are words rather than numbers. In effect, much of FL may be viewed as a methodology for computing with words rather than numbers. Although words are inherently less precise than numbers, their use is closer to human intuition. Furthermore, computing with words exploits the tolerance for imprecision and thereby lowers the cost of solution.

Another basic concept in FL, which plays a central role in most of its applications, is that of a fuzzy if-then rule or, simply, fuzzy rule. Although rule-based systems have a long history of use in Artificial Intelligence (AI), what is missing in such systems is a mechanism for dealing with fuzzy consequents and fuzzy antecedents. In fuzzy logic, this mechanism is provided by the calculus of fuzzy rules. The calculus of fuzzy rules serves as a basis for what might be called the Fuzzy Dependency and Command Language (FDCL). Although FDCL is not used explicitly in the toolbox, it is effectively one of its principal constituents. In most of the applications of fuzzy logic, a fuzzy logic solution is, in reality, a translation of a human solution into FDCL.