Open loop system transfer function

Compute the open-loop response of the following control system model at an analysis point specified by an AnalysisPoint block, X.

Create a model of the system by specifying and connecting a numeric LTI plant model, G, a tunable controller, C, and the AnalysisPoint, X.

G = tf([1 2], [1 0.2 10]); C = tunablePID('C', 'pi'); X = AnalysisPoint('X'); T = feedback(G*X*C, 1);

T is a genss model that represents the closed-loop response of the control system from to . The model contains AnalysisPoint block X, which identifies the potential loop-opening location.

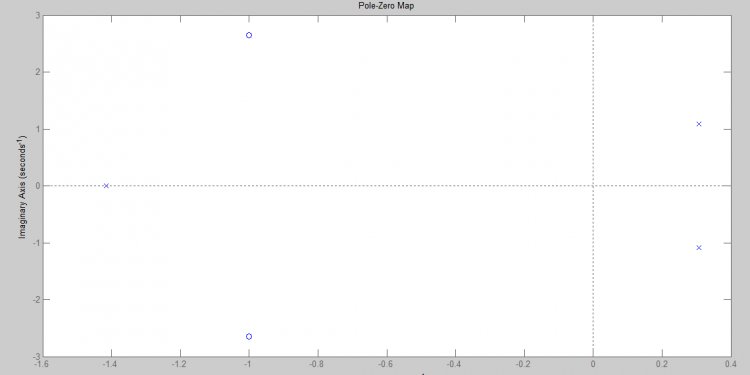
Calculate the open-loop point-to-point loop transfer at location X.

L = getLoopTransfer(T, 'X');

This command computes the positive-feedback transfer function you would obtain by opening the loop at X, injecting a signal into G, and measuring the resulting response at the output of C. By default, getLoopTransfer computes the positive feedback transfer function. In this example, the positive feedback transfer function is

The output L is a genss model that includes the tunable block C. You can use getValue to obtain the current value of L, in which all the tunable blocks of L are evaluated to their current numeric value.