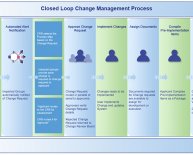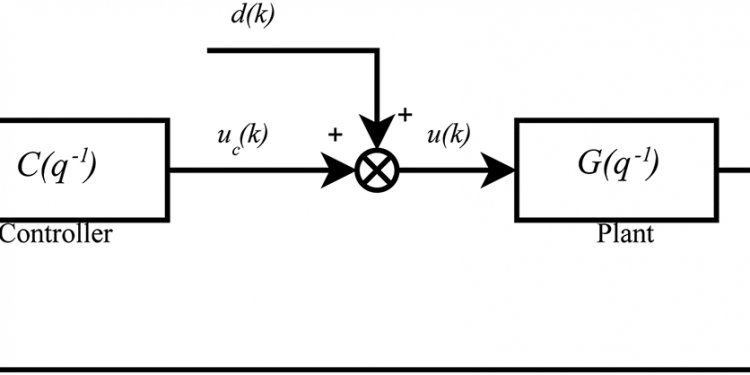
Closed loop control diagram

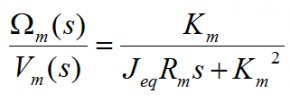Laden Sie Beispielprogramme herunter und gehen Sie nachfolgendes Tutorium durch, um den im obigen Video gezeigten Praktikumsaufbau nachzubilden.

Schritt 1: Modellierung

Die Entwicklung eines Reglers beginnt mit einer mathematischen Beschreibung der Regelstrecke bzw. der Erstellung eines Modells. Modell können von ganz vielen Systemen erstellt werden, darunter mechanische Systeme, elektronische Schaltungen, analoge und digitale Filter sowie Wärme- und Flüssigkeitssysteme. Für dieses Experiment wird ein Modell für einen Gleichstrommotor entwickelt.

Der Gleichstrommotor lässt sich am besten durch eine Übertragungsfunktion darstellen. Eine Übertragungsfunktion liefert eine mathematische Beschreibung dafür, wie die Eingänge und Ausgänge eines Systems miteinander in Beziehung stehen. Im vorliegenden Fall ist der Eingang zum System eine Spannung (Vm) und der Ausgang aus dem System eine Winkelgeschwindigkeit (Ωm). Anhand der nachfolgenden Gleichung lässt sich das Modell des Gleichstrommotors darstellen. Dabei:

Km = Konstante des Motors (V/(rad/s))
Rm = Ankerwiderstand des Motors (Ohm)
Jeq = Ersatzträgheitsmoment (kg*m2) (angenommen, dass Jeq=Jm(Ankerträgheitsmoment des Motors))

Abb. 1: Mathematisches Modell bzw. Übertragungsfunktion für einen Gleichstrommotor

Dieses Modell wird eingesetzt, um einen Regler zu entwerfen, der anschließend mit dem eigentlichen Motor getestet werden kann. Die Übertragungsfunktion kann in LabVIEW mithilfe eines MathScript-Knoten dargestellt werden, der Teil des LabVIEW MathScript RT Module ist. Die Eingangsparameterwerte stammen aus den Spezifikationen des QNET DC Motor von Quanser.

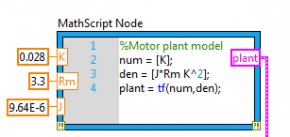Abb. 2: Modell des Gleichstrommotors dargestellt im LabVIEW-MathScript-Knoten

Der MathScript-Knoten befindet sich auf der Palette Programmierung > Strukturen.

Schritt 2: Regelungsentwurf

Als nächster Schritt muss ein Regelungsverfahren ausgewählt und ein Regler entworfen werden. Wenn ein Regler entwickelt wird, ist es sehr hilfreich, die Regelstrecke umfassend zu verstehen: in diesem Fall den Gleichstrommotor. Dies ist über Analysen mit speziellen Grafen, wie Bode- und Nyquist-Diagramme sowie Wurzelortskurven, möglich, die vermuten lassen, wie sich eine Regelstrecke verhalten wird. Grafen im Zeitbereich, wie etwa die Sprungantwort, liefern sofort Feedback über das ideale Verhalten des Systems, z. B. Anstiegszeit, Überschwingung, Einschwingzeit und bleibende Regelabweichung.

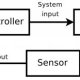
Abb. 3: Schematische Darstellung eines Regelsystems

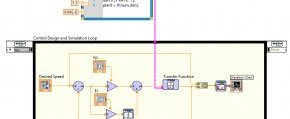
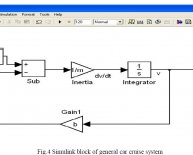
Für dieses Experiment wird ein PI-Regler für den Gleichstrommotor mithilfe des LabVIEW Control Design and Simulation Module erstellt. Die Simulationsschleife, die einen integrierten ODE-Lösungskalkulator für Integral- und Differenzialgleichungen beinhaltet, befindet sich in der Palette Reglerdesign und Simulation unter Simulation. Die Blöcke Summierung, Verstärkung, Integrator und Übertragungsfunktion befinden sich ebenfalls in der Palette Reglerdesign und Simulation unter Simulation > Signal Arithmetic und Simulation > Continuous Linear Systems.

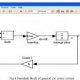
Abb. 4: Regel- und Simulationsschleife in LabVIEW

Schritt 3: Simulation

Der nächste Schritt besteht darin, die Antwort des Gleichstrommotors zu simulieren, wenn der Sollwert oder die gewünschte Geschwindigkeitseingabe verändert werden. Dadurch lassen sich Reglerparameter oder -verstärkungen abstimmen und so die Stabilität des Systems erhöhen. Außerdem müssen die in Schritt 1 erstellte Übertragungsfunktion bzw. das Modell des Gleichstrommotors mit dem Regler kombiniert werden.

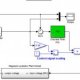
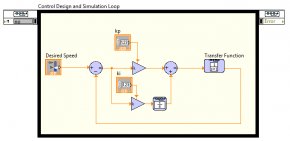Abb. 5: PI-Regler mit Übertragungsfunktion des Gleichstrommotors

Schritt 4: Abstimmung und Verifizierung

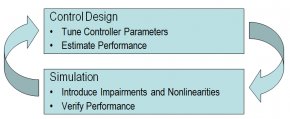
Da nun sowohl Regler und Antwort des Gleichstrommotors simuliert werden können, kann ein iterativer Vorgang zur Optimierung des Reglers befolgt werden. Dazu werden die Reglerparameter vom LabVIEW-Frontpanel abgestimmt und zugleich die Systemleistungen verifiziert.

Abb. 6: Iterativer Vorgang zur Optimierung des Reglers

Anhand der folgenden Schritte können die Regelparameter abgestimmt werden:

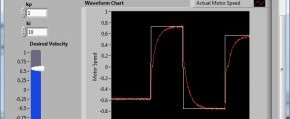
Sobald das Programm ausgeführt wird, sehen wir die gewünschte und die geschätzte Motorgeschwindigkeit auf dem Diagramm. Die Anstiegszeit mit der gewählten proportionalen Verstärkung (kp mit dem Wert 1) sieht gut aus. Allerdings zeigt das Diagramm eine geringe bleibende Regelabweichung, die durch die Lücke zwischen den gewünschten und den geschätzten Geschwindigkeitsdaten dargestellt wird. Diese Abweichung kann über eine Erhöhung der integralen Verstärkung ki verringert werden.

Abb. 7: Simulation der Gleichstrommotorantwort mithilfe eines Proportionalreglers (P)

Wenn die integrale Verstärkung ki auf 10 erhöht wird, ergibt sich eine viel bessere Systemantwort.

Abb. 8: Simulation der Gleichstrommotorantwort mithilfe eines Proportional-Integral-Reglers (PI)

Schritt 5: Implementierung

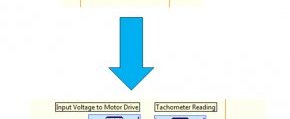
Nachdem verifiziert ist, dass der PI-Regler mit der simulierten Gleichstrommotorantwort funktioniert, können das abschließende Regelsystem implementiert und die Geschwindigkeit der DC-Motor-Steckkarte für NI ELVIS von Quanser geregelt werden. Das LabVIEW Control Design and Simulation Module kann zur Steuerung und Regelung realer Systeme genauso wie für simulierte Modelle verwendet werden. Zur Migration von simulierter zu realer Steuerung und Regelung kann das Regelstreckenmodell durch Hardwareein- und -ausgangsfunktionen ersetzt werden. In diesem Fall wird die Übertragungsfunktion, die den Gleichstrommotor darstellt, durch Ein- und Ausgangs-VIs für die Datenerfassung ersetzt, die den eigentlichen Motor regeln.

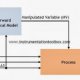
Abb. 9: Migration von Simulation auf reale Hardware durch Ersetzen der Übertragungsfunktion mit Hardwareein- und -ausgangsblöcken

Beim Einsatz der Regel- und Simulationsschleife mit realer Hardware ist das Timing ein wichtiger Faktor. Da sich die Schleife eines integrierten ODE-Solvers mit Zeitschritten bedient, ist es wichtig, die Simulations- und die Timing-Parameter der Schleife auf denselben Zeitschritt einzustellen. Datenerfassungsaufgaben nutzen meist Timing-Parameter, deshalb muss auch das Timing der Simulationsschleife mit dem der Datenerfassung übereinstimmen.

Jetzt können das LabVIEW-Programm ausgeführt und die Geschwindigkeit des DC-Motors von Quanser vom LabVIEW-Frontpanel aus gesteuert werden.