Steady State Response control system

it is very essential to know a few basic terms and these are described below. Standard Input Signals : These are also known as test input signals. The input signal is very complex in nature, it is complex because it may be a combination of various other signals. Thus it is very difficult to analyze characteristic performance of any system by applying these signals. So we use test signals or standard input signals which are very easy to deal with. We can easily analyze the characteristic performance of any system more easily as compared to non standard input signals. Now there are various types of standard input signals and they are written below:

Unit Impulse Signal : In the time domain it is represented by ∂(t). The Laplace transformation of unit impulse function is 1 and the corresponding waveform associated with the unit impulse function is shown below. Now are in a position to describe the two types of responses which are a function of time.

Transient Response of Control System

As the name suggests transient response of control system means changing so, this occurs mainly after two conditions and these two conditions are written as follows-

• Condition one : Just after switching ‘on’ the system that means at the time of application of an input signal to the system.
• Condition second : Just after any abnormal conditions. Abnormal conditions may include sudden change in the load, short circuiting etc.

Steady State Response of Control System

Steady state occurs after the system becomes settled and at the steady system starts working normally. Steady state response of control system is a function of input signal and it is also called as forced response. Now the transient state response of control system gives a clear description of how the system functions during gives a clear description of how the system functions during steady state. Therefore the time analysis of both states is very essential. We will separately analyze both the types of responses. Let us first analyze the transient response. In order to analyze the transient response, we have some time specifications and they are written as follows: Delay Time : This time is represented by td. The time required by the response to reach fifty percent of the final value for the first time, this time is known as delay time. Delay time is clearly shown in the time response specification curve. Rise Time : This time is represented by tr. We define rise time in two cases:

1. In case of under damped systems where the value of ζ is less than one, in this case rise time is defined as the time required by the response to reach from zero value to hundred percent value of final value.
2. In case of over damped systems where the value of ζ is greater than one, in this case rise time is defined as the time required by the response to reach from ten percent value to ninety percent value of final value.

Peak Time : This time is represented by tp. The time required by the response to reach the peak value for the first time, this time is known as peak time. Peak time is clearly shown in the time response specification curve.

Settling Time : This time is represented by ts. The time required by the response to reach and within the specified range of about (two percent to five percent) of its final value for the first time, this time is known as settling time. Settling time is clearly shown in the time response specification curve.

Maximum Overshoot : It is expressed (in general) in percentage of the steady state value and it is defined as the maximum positive deviation of the response from its desired value. Here desired value is steady state value.

Steady State Error : It can be defined as the difference between the actual output and the desired output as time tends to infinity.

Now we are in position we to do a time response analysis of a first order system.

Transient State and Steady State Response of First Order Control System

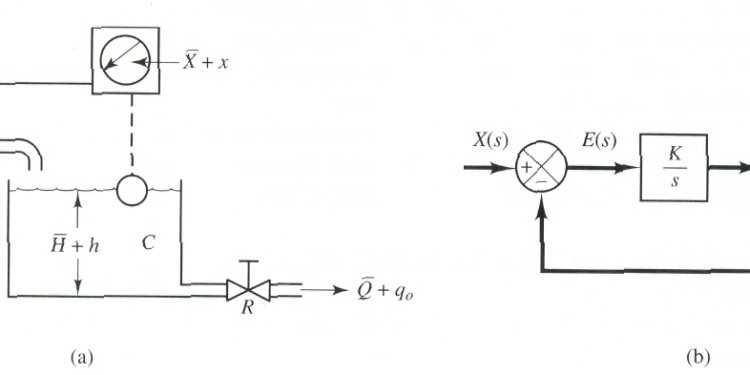
Let us consider the block diagram of the first order system. From this block diagram we can find overall transfer function which is linear in nature. The transfer function of the first order system is 1/((sT+1)). We are going to analyze the steady state and transient response of control system for the following standard signal.

1. Unit impulse.
2. Unit step.
3. Unit ramp.

Unit impulse response : We have Laplace transform of the unit impulse is 1. Now let us give this standard input to a first order system, we have Now taking the inverse Laplace transform of the above equation, we have It is clear that the steady state response of control system depends only on the time constant ‘T’ and it is decaying in nature.

Unit step response : We have Laplace transform of the unit impulse is 1/s. Now let us give this standard input to first order system, we have With the help of partial fraction, taking the inverse Laplace transform of the above equation, we have It is clear that the time response depends only on the time constant ‘T’. In this case the steady state error is zero by putting the limit t is tending to zero.

Unit ramp response : We have Laplace transform of the unit impulse is 1/s2. Now let us give this standard input to first order system, we have With the help of partial fraction, taking the inverse Laplace transform of the above equation we have On plotting the exponential function of time we have ‘T’ by putting the limit t is tending to zero.

Transient State and Steady State Response of Second Order Control System

Let us consider the block diagram of the second order system. From this block diagram we can find overall transfer function which is nonlinear in nature. The transfer function of the second order system is (ω2) / ( s ( s + 2ζω )). We are going to analyze the transient state response of control system for the following standard signal. Unit impulse response : We have Laplace transform of the unit impulse is 1. Now let us give this standard input to second order system, we have Where ω is natural frequency in rad/sec and ζ is damping ratio.

Unit step response : We have Laplace transform of the unit impulse is 1/s. Now let us give this standard input to first order system, we have Now we will see the effect of different values of ζ on the response. We have three types of systems on the basis of different values of ζ.